
图像语义分割实践(五)优化器与学习率
时间:2024-08-12 来源:网络 人气:
在数据制作环节中,提到minibatch思想用于数据批次量获取,是一种优化器思想,而该文则是对各种优化器进行介绍。
优化器:最小化损失函数算法,把深度学习当炼丹的话,优化器就是炉子,决定火候大小,炉子属性等,在深度学习监督学习的模型中,常用梯度下降法求解最优参数;
学习率:在优化器中,决定着梯度下降的速度,炉子调整火候的时间点;
Pytorch中,torch.optim 提供优化器类型选择,torch.optim.lr_scheduler 提供学习率调整策略;
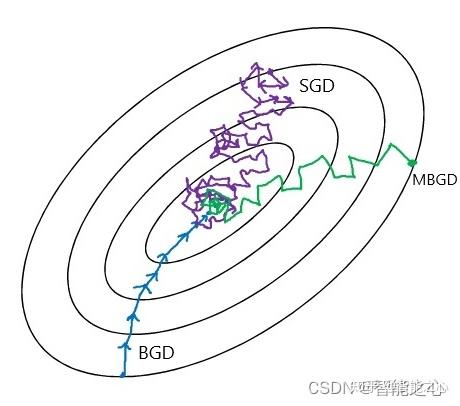
梯度下降方法(Gradient Descent)变体如图所示,BGD全样本训练,计算量太大,计算速度慢;SGD太过震荡,容易陷入鞍点找不到最优点;MBGD训练稳定,计算速度快;
SGD 公式 即使采用MBGD的方法仍然有很大难题,还不能保证良好的收敛性。
- 学习率选择和设计问题;
- 参数更新都在同一个学习率下更新的,实际训练特征出现频率少的需要更大的学习率;
由 SGD -> Momentum Momentum,动量法, 除了保留$?θJ(θ{t?1})$该位置的梯度向量,同时加入$v_{t?1}$考虑上一次梯度向量,保证更新的梯度方向不会过分偏离上一次梯度,从而方向抖动不会很明显,前进方向由惯性动量决定,因此,$γ$称为动量超参。可以看出,缺陷还是很明显的,所有参数还是无法逃离共享同一个学习率的命运。
由 Momentum -> Nesterov Accelerated Gradient Nesterov Accelerated Gradient,NAG加速动量法,当前位置梯度加入$-γv_{t?1}$近似预测未来的权重,部分RNN网络上表现良好,比Momentum震荡幅度会小,“冲坡”不至于太快 。
# NAG加速动量法
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3, momentum=0.9, nesterov=True)
Adagrad(Adaptive Gradient 自适学习率应梯度下降) 其中,$\\Delta θ_t$项是 $θ_t$ 的差值,更新较频繁的$θ_t$累计的$n_t$越大,分母越大,学习率变小,从而$θ_i$的学习率就调小。因此,$Adagrad$对于更新频率较低的参数用较大的学习率,对于更新频率较高的参数用较小的学习率。
有的时候学习速率收敛的过快会导致模型在训练到局部最优解前就停止参数更新。为了解决这个问题,人们提出了RMS Prop梯度下降法
Adadelta & Rmsprop 优点是不需要指定学习率
Adaptive Moment Estimation(Adam) 本质是带 Momentum 的 RMSProp 方法,新手推荐该方法,万金油。
# Adam
optimizer=torch.optim.SGD(model.parameters(), lr=1e-3, momentum=0.9, nesterov=True)
PyTorch提供的学习率调整策略分为三大类,分别是
- 有序调整:等间隔调整(Step),按需调整学习率(MultiStep),指数衰减调整(Exponential)和余弦退火(CosineAnnealing)。
- 自适应调整:自适应调整学习率 ReduceLROnPlateau。
- 自定义调整:自定义调整学习率 LambdaLR。
注:PyTorch提供的学习率调整策略, 学习率调整策略接在优化器后头即可,torch.optim.lr_scheduler为代码接口。
# 对构建的模型选择 optimizer :: torch.optim
optimizer=torch.optim.Adam(model.parameters(), lr=1e-3)
# 对optimizer选择 learning_rate :: torch.optim.lr_scheduler
scheduler=torch.optim.lr_scheduler.StepLR(optimizer, step_size=500, gamma=0.9)
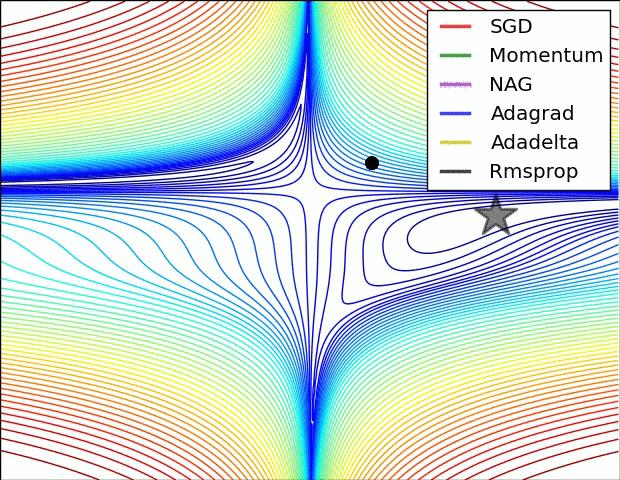
各类 optimizer 的原理
自适应学习率优化器伪代码
优化器推导公式
优化器文字描述推荐
优化器方法
pythorch优化器学习率写法
md符号
【Pytorch 】笔记七:优化器源码解析和学习率调整策略
【Pytorch 】笔记六:初始化与18种损失函数的源码解析
kaggle学习率示例:https://www.kaggle.com/code/isbhargav/guide-to-pytorch-learning-rate-scheduling/notebook
教程资讯
系统教程排行













