
《优化算法》人工鱼群算法学习 超详细解析 附JAVA和matlab示例
时间:2024-08-26 来源:网络 人气:
人工鱼群算法为山东大学副教授李晓磊2002年从鱼找寻食物的现象中表现的种种移动寻觅特点中得到启发而阐述的仿生学优化方案。
在一片水域中,鱼往往能自行或尾随其他鱼找到营养物质多的地方,因而鱼生存数目最多的地方一般就是本水域中营养物质最多的地方,人工鱼群算法就是根据这一特点,通过构造人工鱼来模仿鱼群的觅食、聚群及追尾行为,从而实现寻优。
人工鱼拥有以下几种典型行为:
- 觅食行为:一般情况下鱼在水中随机地自由游动,当发现食物时,则会向食物逐渐增多的方向快速游去。
- 聚群行为: 鱼在游动过程中为了保证自身的生存和躲避危害会自然地聚集成群,鱼聚群时所遵守的规则有三条:
分隔规则:尽量避免与临近伙伴过于拥挤;
对准规则:尽量与临近伙伴的平均方向一致;
内聚规则:尽量朝临近伙伴的中心移动。 - 追尾行为:当鱼群中的一条或几条鱼发现食物时,其临近的伙伴会尾随其快速到达食物点。
- 随机行为:单独的鱼在水中通常都是随机游动的,这是为了更大范围地寻找食物点或身边的伙伴。
人工鱼群算法实现的步骤:
- 初始化设置,包括种群规模N、每条人工鱼的初始位置、人工鱼的视野Visual、步长step、拥挤度因子δ、重复次数Trynumber;
- 计算初始鱼群各个体的适应值,取最优人工鱼状态及其值赋予给公告牌;
- 对每个个体进行评价,对其要执行的行为进行选择,包括觅食Pray、聚群Swarm、追尾Follow和评价行为bulletin;
- 执行人工鱼的行为,更新自己,生成新鱼群;
- 评价所有个体。若某个体优于公告牌,则将公告牌更新为该个体;
- 当公告牌上最优解达到满意误差界内或者达到迭代次数上限时算法结束,否则转步骤3。


人工鱼群算法有5个基本参数:群规模N、人工鱼的视野Visual、步长Step、拥挤度因子δ、重复次数Trynumber。
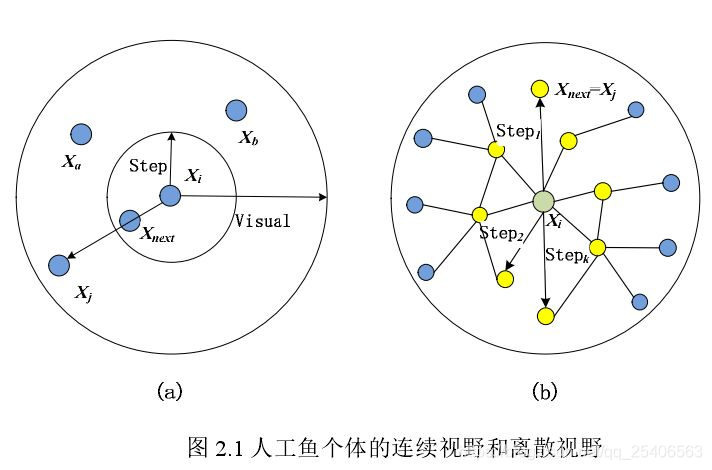
动物的观察力是及其深奥的,它可以很快的洞察到周边的物体,鱼类的视野中分为连续型视野和离散型视野两类。应用如下方法实现虚拟人工鱼的视觉:
图2.1(a)表示具有连续型视野的一条假设的人工鱼个体,它能看到的区域 Visual 为以现在位置 Xi为圆心一定距离为半径的圆形区域,地点 Xj为它在一个时候巡视到的视点种另一地方,如果这个地点的食物量比之前地方的多,就决定去这个地方前进步长的随机数达到地点 Xnext;
人工鱼的离散型视野为与节点位置 Xi 相邻且相通的所有节点,如图 2.1(b)所示,根据判断边的代价来选择下一步位置 Xnext。
由于视野对算法中个行为都有较大影响,因此,它的变化对收敛性能影响也比较复杂。
当视野范围较小时,人工鱼的觅食行为和随机行为比较突出;视野范围较大时,人工鱼的追尾行为和聚群行为将变得比较突出,相应的算法的复杂度也会有所上升。
总的来说:视野越大,越容易使人工鱼发现全局最优解并收敛。
对于固定步长,随着步长的增加,收敛的速度得到了一定的加速,但在超过一定的范围后,有使得收敛速度减缓,步长过大时会出现震荡现象而大大影响收敛速度。
采用随机步长的方式在一定程度上防止了震荡现象的发生,并使得该参数的敏感度大大降低了,但最快的收敛速度还是最优固定步长的收敛速。
所以,对于特定的优化问题,我们可以考虑采用合适的固定步长或者变尺度方法来提高收敛速度。
人工鱼的数目越多,跳出局部最优解的能力越强,同时,收敛的速度也越快。
当然,付出的代价就是算法每次迭代的计算量也越大,因此,在使用过程中,满足稳定收敛的前提下,应当尽可能的减少个体数目。
尝试次数越多,人工鱼的觅食行为能力越强,收敛的效率也越高。
在局部极值突出的情况下,应该适当的减少以增加人工鱼随机游动的概率,克服局部最优解。
在求极大值问题中,δ=1/(αnmax),α∈(0,1]δ=1/(αnmax),α∈(0,1];在求极小值问题中,δ=αnmax,α∈(0,1]δ=αnmax,α∈(0,1]。其中α为极值接近水平, nmax为期望在该邻域内聚集的最大人工鱼数目。
拥挤度因子与nf相结合,通过人工鱼是否执行追尾和聚群行为对优化结果产生影响。以极大值为例(极小值的情况正好与极大值相反),δ越大,表明允许的拥挤程度越小,人工鱼摆脱局部最优解的能力越强;但是收敛速度会有所减缓,这主要因为人工鱼在逼近最优解的同时,会因避免过分拥挤而随机走开或者受其他人工鱼的排斥作用,不能精确逼近极值点。
可见,虽然δ的引入避免了人工鱼过度拥挤而陷入局部最优解,但是另一方面,该参数会使得位于极值点附件的人工鱼之间存在相互排斥的影响,而难以想极值点精确逼近。
所以,对于某些局部极值不是很严重的具体问题,可以忽略拥挤的因素,从而在简化算法的同时也加快算法的收敛速度和提高结果的精确程度。
- 群规模:N越大收敛越快,越容易寻得全局最优解,但是计算量越大;
- 感知范围:视野越大,越易发现全局最优解;
- 步长:决定收敛速度;
- 拥挤因子:适当选择可避免局部最优
- 重复次数:越大收敛越快,可调整随机游走概率,克服局部最优解
人工鱼有四种基本行为,包括觅食Pray、聚群Swarm、追尾Follow和评价行为bulletin。
这是鱼趋向食物的一种活动,一般认为它是通过视觉或味觉来感知水中的食物量或食物浓度来选择行动的方向。
设置人工鱼当前状态,并在其感知范围内随机选择另一个状态,如果得到的状态的目标函数大于当前的状态,则向新选择得到的状态靠近一步,反之,重新选取新状态,判断是否满足条件。
选择次数达到一定数量后,如果仍然不满足条件,则随机移动一步。

大量或少量的鱼聚集成群,进行集体觅食和躲避敌害,这是它们在进化过程中形成的一种生存方式。
人工鱼探索当前邻居内的伙伴数量,并计算伙伴的中心位置,然后把新得到的中心位置的目标函数与当前位置的目标函数相比较,如果中心位置的目标函数优于当前位置的目标函数并且不是很拥挤,则当前位置向中心位置移动一步,否则执行觅食行为。
鱼聚群时会遵守两条规则:一是尽量向邻近伙伴的中心移动,二是避免过分拥挤。

当某一条鱼或几条鱼发现食物时,它们附近的鱼会尾随而来,导致更远处的鱼也会尾随过来。
人工鱼探索周围邻居鱼的最优位置,当最优位置的目标函数值大于当前位置的目标函数值并且不是很拥挤,则当前位置向最优邻居鱼移动一步,否则执行觅食行为。

它是觅食行为的一个缺省行为,指人工鱼在视野内随机移动。当发现食物时,会向食物逐渐增多的方向快速的移动。
公告牌是记录最优人工鱼个体状态的地方。每条人工鱼在执行完一次迭代后将自身当前状态与公告牌中记录的状态进行比较,如果优于公告牌中的状态则用自身状态更新公告牌中的状态,否则公告牌的状态不变。
当整个算法的迭代结束后,公告牌的值就是最优解。
行为评价是用来反映鱼自主行为的一种方式,在解决优化问题时选用两种方式评价:一种是选择最优行为执行;另一种是选择较优方向。
对于解决极大值问题,可以使用试探法,即模拟执行群聚、追尾等行为,然后评价行动后的值选择最优的来执行,缺省的行为为觅食行为。
一般通过试探法,模拟执行上述几种行为,评价后选择最大者实行;
迭代终止条件:
-
通常的方法是判断连续多次所得值得均方差小鱼允许的误差;
-
或判断聚集于某个区域的人工鱼的数目达到某个比例;
-
或连续多次所得的均值不超过已寻找的极值;
-
或限制最大迭代次数。
若满足终止条件,则输出公告牌的最优记录;否则继续迭代。
求解x2-160x+640+y2-260y+16900这个二元函数的最小值;
一元函数的优化实例:
m
a
x
f
(
x
)
=
x
s
i
n
(
10
π
x
)
+
2.0
maxf(x) = xsin(10πx) + 2.0
maxf(x)=xsin(10πx)+2.0
s.t.
1
≤
x
≤
2
1 ≤ x ≤ 2
1≤x≤2
二元函数的优化实例:
m
a
x
f
(
x
,
y
)
=
s
i
n
x
x
s
i
n
y
y
maxf(x,y) = \frac{sinx}{x} \frac{siny}{y}
maxf(x,y)=xsinx?ysiny?
s.t.
x
∈
[
?
10
,
10
]
x\in[-10,10]
x∈[?10,10]
y
∈
[
?
10
,
10
]
y\in[-10,10]
y∈[?10,10]
具体的源代码放到文末:有需要的同学可以自行查看学习。
| 序号 | 函数名 | 函数功能 |
|---|---|---|
| 1 | AF_init | 初始化鱼群函数 |
| 2 | AF_prey | 觅食行为函数 |
| 3 | AF_swarm | 聚群行为函数 |
| 4 | AF_follow | 追尾行为函数 |
| 5 | AF_dist | 计算鱼群个体距离函数 |
| 6 | AF_foodconsistence | 当前位置的事物浓度函数 |
初始化鱼群函数AF_init
初始化鱼群函数AF_prey
初始化鱼群函数AF_swarm
初始化鱼群函数AF_follow
初始化鱼群函数AF_dist
初始化鱼群函数AF_foodconsistence
计算鱼群距离 dist
教程资讯
WinXp教程排行













